- Сравнение дробей с одинаковыми знаменателями
- Сравнение дробей с одинаковыми числителями
- Сравнение смешанных и неправильных дробей с правильными дробями
- Сравнение двух смешанных дробей
- Сравнение дробей с разными числителями и знаменателями
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями, но разными числителями больше та дробь, у которой числитель больше, например:

Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями, но разными знаменателями больше та дробь, у которой знаменатель меньше, например:
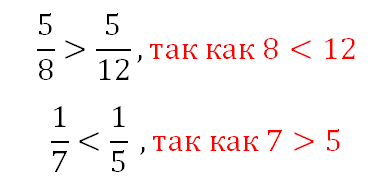
Сравнение смешанных и неправильных дробей с правильными дробями
Неправильная или смешанная дробь всегда больше правильной дроби, например:
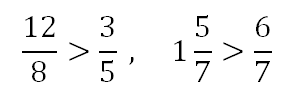
Это правило исходит из того, что правильная дробь всегда меньше 1, а смешанная или неправильная дробь (которую всегда можно перевести в смешанную, выделив целую часть), уже содержит одну или больше единиц (целых частей).
Сравнение двух смешанных дробей
При сравнении двух смешанных дробей больше та дробь, у которой целая часть больше, например:

Если целые части у смешанных дробей одинаковые, больше та дробь, у которой дробная часть больше, например:

Сравнение дробей с разными числителями и знаменателями
Сравнивать дроби с разными числителями и знаменателями без их преобразования нельзя. Сначала дроби нужно привести к одному знаменателю, а затем сравнить их числители. Больше та дробь, у которой числитель будет больше. Читайте статью «Как привести дроби к одному знаменателю».
