Из этой статьи вы узнаете:
- Что такое квадратные уравнения
- Коэффициенты квадратного уравнения
- Неполные квадратные уравнения и их решение
- Приведённое квадратное уравнение
- Решение квадратного уравнения. Дискриминант
- Формула корней квадратного уравнения
Что такое квадратные уравнения
Квадратные уравнения — это уравнения вида ax2 + bx + c = 0
где x — переменная, a, b, c — некоторые числа, причем a ≠ 0 .
Коэффициенты квадратного уравнения
Числа a, b, c называют коэффициентами уравнения, причем каждое из них имеет свое название:
Число а называют первым (или старшим) коэффициентом. Число b — вторым коэффициентом, а число c — свободным членом.
Пример 1:
квадратное уравнение – 3x2 + 4x + 7 = 0 имеет следующие коэффициенты :
a = –3, b = 4, c = 7.
Пример 2:
квадратное уравнение 6x2 – 4x – 7 = 0 имеет следующие коэффициенты :
a = 6, b = –4, c = –7.
Неполные квадратные уравнения и их решение
Если в квадратном уравнении хотя бы один из коэффициентов b и c равен нулю, то такое уравнение называется неполным.
Существует три вида неполных квадратных уравнений:
- ax2 = 0 ( в случае, когда b = 0, с = 0)
- ax2 + bx = 0 ( в случае, когда b ≠ 0, с = 0)
- ax2 + c = 0 ( в случае, когда b = 0, с ≠ 0)
Неполные квадратные уравнения легко решаются, рассмотрим решение каждого вида:
ax2 = 0
Поскольку a ≠ 0, то данное уравнение имеет всего один корень x = 0.
Например, квадратное уравнение –19 x2 = 0 имеет один корень : x = 0.
ax2 + bx = 0
Для решения такого уравнения выносят x за скобки и получают уравнение вида
x (ax + b) = 0
Это уравнение имеет всегда два корня (так как в левой части у нас два множителя x и (ax + b), а если хотя бы один из множителей равен нулю, то и все произведение равно нулю) .
x1 = 0, а x2 можно найти, решив простое линейное уравнение в скобках :
ax + b = 0
ax = –b
x2 = –b/a
Например, решим квадратное уравнение 5x2 + 2x = 0
x(5x + 2)= 0 Сразу напишем, что x1 = 0. Далее найдем x2.
Для этого решим уравнение 5x + 2 = 0
5x = –2
x = –2/5
Ответ: x1 = 0, x2 = –2/5
ax2 + c = 0
Это уравнение также нужно преобразовать:
ax2 =–c
x2 = –c/a
Так как с ≠ 0, то возможны два случая: –c/a < 0, и –c/a > 0.
В первом случае уравнение x2 = –c/a корней не имеет, так как квадрат числа всегда положительный. Во втором случае, то есть когда –c/a > 0, уравнение имеет два корня:
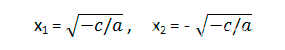
Пример 1:
2x2 + 8 = 0
2x2 = -8
x2 = –8/2
x2 = –4 Корней нет.
Пример 2:
3x2 – 15 = 0
3x2 = 15
x2 = 15/3
x2 = 5
![]()
Приведённое квадратное уравнение
Если в квадратном уравнении коэффициент a = 1, то такое уравнение называют приведённым. Приведенные уравнения также могут быть неполными.
Примеры приведённых уравнений:
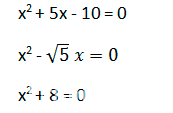
Любое неприведённое квадратное уравнение можно преобразовать в приведённое, разделив обе части уравнения на коэффициент a, (поскольку в левой части уравнения сумма, то на а делим каждое слагаемое):
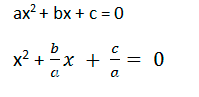
Пример 1:
Преобразуем неприведённое квадратное уравнение 2x2 – 6x + 8 = 0 в приведённое, для этого делим левую и правую часть уравнения на 2, получаем приведённое уравнение:
x2 – 3x + 4 = 0
Пример 2:
–4x2 + 12x = 0 Делим обе части уравнения на -4, и получаем приведённое уравнение:
x2 – 3x = 0
Решение квадратного уравнения ax2 + bx + c = 0
Для того, чтобы решить квадратное уравнение, нужно сначала найти его дискриминант (D) по формуле:
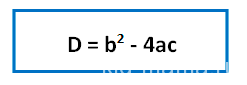
При этом возможны три случая:
- D < 0
- D = 0
- D > 0
__________________________________________________
- Если D < 0, то уравнение корней не имеет.
- Если D = 0, то уравнение имеет один корень :
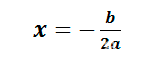
- Если D > 0, то уравнение имеет два корня:
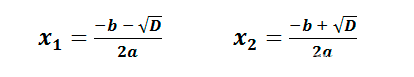
————————————————————————————————————-
Формула корней квадратного уравнения выглядит так: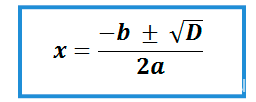
Эта формула подходит и для второго случая, когда D = 0, так как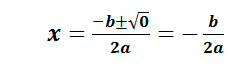
Алгоритм решения квадратного уравнения
- Найти дискриминант D
- Если D < 0, написать, что корней нет
- Если D ≥ 0 , найти корни по формуле корней квадратного уравнения.
_________________________________________________________________
Пример 1:![]()
Для данного уравнения a = 3, b = -2, с = -16
Дискриминант уравнения:![]()
Дискриминант больше нуля, находим корни: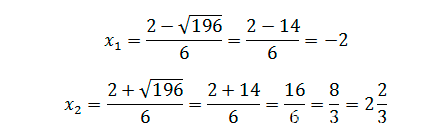
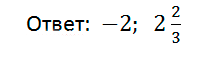
Пример 2 :![]()
Для данного уравнения a = -0,5 b = 2 c = -2
Дискриминант уравнения:![]()
Уравнение имеет один корень. Найдем его:
Пример 3 :![]()
Для данного уравнения a = 1 b = -6 c = 11
Дискриминант уравнения:![]()
Дискриминант D<0, корней нет
Ответ: корней нет.
