Содержание статьи:
- Что такое десятичные дроби
- Сравнение десятичных дробей
- Сложение и вычитание десятичных дробей
- Умножение и деление десятичных дробей
- Округление чисел
Что такое десятичные дроби
Десятичные дроби — это особая запись дробных чисел. Выглядят они так:
Обыкновенные дроби, знаменатели которых равны 10, 100, 1000, 10000 и т.д., (то есть единица с одним или несколькими нулями), можно записать в виде десятичных дробей, без знаменателя. 
Как правильно записать десятичную дробь? Сначала пишется целая часть дроби или ноль, если дробь правильная, затем ставится запятая, а после запятой записывается числитель дроби, и здесь нужно быть очень внимательными. Дело в том, что количество знаков после запятой должно быть равно количеству нулей в знаменателе обыкновенной дроби. А в числителе может быть меньше цифр, чем надо. В этом случае мы приписываем к числителю нули, добавляя их не в конце числа, а сразу после запятой, то есть перед числителем:
Как видите, ничего сложного. Читаются десятичные дроби так же, как они читались бы в виде обыкновенных дробей: три целых, две десятых, шесть целых сорок четыре сотых, ноль целых двадцать три десятитысячных.
Чтобы правильно назвать дробь, считают количество знаков после запятой. Один знак — десятые, два знака — сотые, три знака — тысячные и т.д.
Теперь одно важное уточнение: нули в конце десятичной дроби не имеют никакого значения и отбрасываются. Мы можем приписать сколько угодно нулей, и при этом дробь не изменится:
Запомните это свойство десятичных дробей, так как оно нам пригодится при сложении и вычитании столбиком, а также при сравнении дробей.
Сравнение десятичных дробей
При сравнении десятичных дробей больше та дробь, у которой целая часть больше. 
Если же у дробей целые части равны, поступают следующим образом:
- Считают количество знаков после запятой у обоих чисел, и если оно не одинаковое, то уравнивают их, приписывая нули в конце одной из дробей.
- Переписывают полученные числа без запятых и сравнивают их. Эту операцию можно проводить мысленно, в уме:
Сложение и вычитание десятичных дробей
Десятичные дроби складывают столбиком так же, как обыкновенные числа, при этом их записывают так, чтобы запятая находилась строго под запятой. Далее следуют алгоритму:
- Количество знаков после запятой уравнивают, приписывая нули на конце дроби.
- Выполняют сложение или вычитание как обычно, не обращая внимания на запятую.
- Ставят запятую под запятой в данных дробях.
Если вы складываете целое число и десятичную дробь, то просто прибавляете это число к целой части, которая находится перед запятой. Например:
5 + 2,43 = 7,43
74 + 0,004 = 74,004
Если нужно из целого числа вычесть десятичную дробь, то уравниваете количество знаков после запятой и вычитаете столбиком, как описано в начале этой статьи. Например, как выполнить вычитание 52 — 3,614 = ?
Умножение и деление десятичных дробей
Умножение десятичных дробей на натуральное число
Чтобы умножить десятичную дробь на целое число, надо умножить её на это число, не обращая внимание на запятую, а затем в полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби.
Например:
2 · 0,34 = 0,68
5 · 0,002 = 0,010 = 0,01 (нули на конце десятичной дроби отбрасываются)
Умножение десятичных дробей на 10, 100, 1000, 10 000 и т. д.
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.
Например:
8,963 · 10 = 89,63
0,062 · 1000 = 0062 = 62 (нули перед числом не пишутся)
2,9 · 10000 = 2,9000 · 10000 = 29000
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
- Выполнить умножение, не обращая внимания на запятые.
- Отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.
Деление десятичной дроби на натуральное число
Чтобы разделить десятичную дробь на натуральное число, надо:
Разделить дробь на это число, не обращая внимания на запятую. При этом, как только кончится деление целой части, и мы должны будем сносить цифру после запятой, в частном ставим запятую.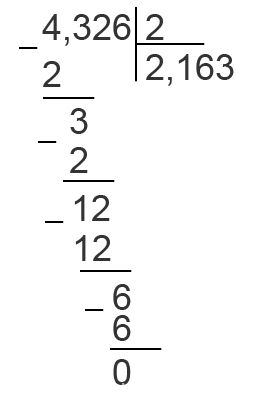 
Если целая часть меньше делителя, ответ начинается с нуля целых.
Деление десятичной дроби на 10, 100, 1000
Для того, чтобы разделить десятичную дробь на 10, 100, 1000, …, надо перенести запятую в этой дроби на столько знаков влево, сколько нулей стоит после единицы в делителе.
При этом иногда приходится сначала написать перед целой частью нуль или несколько нулей.
Например:
374,5 : 100 = 3,745
5,021 : 1000 = 0005,021 : 1000 = 0,005021
0,1 : 100 = 000,1 : 100 = 0,001
Умножение десятичной дроби на 0,1; 0,01; 0,001 и т.д.
Умножить число на 0,1; 0,01; 0,001 и т.д. — это то же самое, что разделить его на 10, 100, 1000 и т.д. Для этого нужно перенести запятую в этой дроби на столько знаков влево, сколько нулей стоит перед единицей в множителе (нуль перед запятой тоже считаем).
Например:
54,3 · 0,1 = 54,3 : 10 = 5,43
0,1 · 0,01 = 0,1 : 100 = 000,1 : 100 = 0,001
Деление на десятичную дробь
Чтобы разделить число на десятичную дробь, надо
- Избавиться от запятой в делителе. Для этого в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
- После этого выполнить деление на натуральное число.
Пример 1:
Разделим 12,096 на 2,24. Перенесём в обоих числах запятую на две цифры вправо. Получим числа 1209,6 и 224. Выполним деление столбиком.
12,096 : 2,24 = 1209,6 : 224 = 5,4
Пример 2:
Разделим 4,5 на 0,125. Перенесём и в делимом, и в делителе запятую на три цифры вправо. Так как у числа 4,5 только одна цифра после запятой, то припишем ему справа два нуля. Получим числа 4500 и 125. Делим столбиком: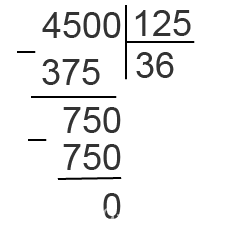
Так как 4500 : 125 = 36, то и 4,5 : 0,125 = 36.
Пример 3:
Разделим 25 на 0,05. Нам нужно перенести запятую в делимом и делителе на два знака вправо. Но число 25 целое, как быть с запятой? Любое целое число можно записать с запятой, приписав после неё сколько угодно нулей. 25 = 25,00. Перенеся запятую на два знака, получим число 2500.
25 : 0,05 = 2500 : 5 = 500
Деление десятичной дроби 0,1; 0,01; 0,001 и т.д.
Разделить число на 0,1; 0,01; 0,001 и т.д. — это то же самое, что умножить его на 10, 100, 1000 и т.д. Для этого нужно перенести запятую в делимом на столько знаков вправо, сколько нулей стоит в делителе перед единицей (ноль перед запятой тоже считаем).
Если цифр не хватает, надо сначала приписать в конце дроби несколько нулей.
Например:
54,87 : 0,1 = 548,7
34,56 : 0,0001 = 34,5600 : 0,0001 = 345600
24 : 0,001 = 24,000 : 0,001 = 24000
Округление чисел
Округление числа — это замена его близким по значению числом с нулями на конце. Число, полученное при округлении, называют приближённым значением данного числа (знак ≈ ) . Округляют как натуральные числа, так и десятичные дроби.
Округление натуральных чисел
Натуральные числа округляют до десятков, сотен, тысяч и т.д. При этом пользуются следующим алгоритмом:
- Находят в числе цифру разряда, до которого нужно округлить число (в примерах она выделена красным)
- Смотрят, какая цифра стоит после неё. Если это цифра 5, 6, 7, 8 или 9, то цифру разряда увеличивают на единицу, а все последующие цифры заменяют нулями. Если же после цифры разряда стоит 4, 3, 2, 1 или 0, то просто заменяют все последующие цифры нулями.
Пример 1:
Округлить число 32748 до сотен. Цифра разряда сотен 7. После неё стоит 4. Значит 32748 ≈ 32700
Пример 2:
Округлить число 1268932 до тысяч. Цифра разряда тысяч 8. После неё стоит 9. Значит, увеличиваем 8 на единицу:
1268932 ≈ 1269000
Пример 3:
Как быть, если рядом стоят несколько девяток?
Округлить число 8269999 до десятков. Цифра разряда десятков 9. После неё стоит 9. Значит, увеличиваем 9 на единицу (и соответственно последующие девятки тоже):
8269999 ≈ 8270000
[spacer height=»5px» id=»5″]
Округление десятичных дробей
Десятичные дроби округляют до целых, до десятых, до сотых, до тысячных и т. д. При этом пользуются тем же самым алгоритмом, но все последующие цифры не заменяют нулями, а отбрасывают, так как они стоят после запятой на конце числа.
Пример 1:
Округлить число 86,2759 до десятых. Цифра разряда десятых 2. После неё стоит 7. Значит, увеличиваем 2 на единицу:
86,2759 ≈ 86,3
Пример 2:
Округлить число 0,372148 до тысячных. Цифра разряда тысячных 2. После неё стоит 1.
0,372148 ≈ 0,372
Пример 3:
Округлить число 5,3721до целых. Цифра разряда целых 5. После неё стоит 3.
5,3721 ≈ 5
